Vedant Asati

Alpha-Beta Pruning: A Deep Dive into its History, Implementation, and Functionality

8 min

Table of Contents

Introduction

Alpha-beta pruning is a pivotal optimization technique used in computer science and artificial intelligence (AI), particularly within the realm of game theory. Its primary function is to reduce the number of nodes evaluated in a decision tree during a minimax search, making it an essential tool for adversarial games like Chess, Checkers, and Go. By eliminating branches that are not necessary for decision-making, alpha-beta pruning allows algorithms to evaluate the most important moves without wasting resources on irrelevant possibilities.

In this blog, we’ll explore the history, implementation, and working of alpha-beta pruning, as well as its role in AI and game theory.

A Glimpse into the History of Alpha-Beta Pruning

The origins of alpha-beta pruning date back to the mid-20th century, during the early development of artificial intelligence. It was first proposed by John McCarthy, a pioneer in AI, although the concept had been independently discovered by multiple researchers around the same time. Initially applied in the context of game trees, alpha-beta pruning was designed to optimize the minimax algorithm — a decision rule used in two-player games to minimize the possible loss while maximizing the potential gain. While the basic minimax algorithm evaluates all possible moves to find the best outcome, alpha-beta pruning accelerates this process by discarding paths that won’t affect the final decision, thereby making the search more efficient. Despite its simplicity, this technique has had a profound impact on AI’s ability to make quick and intelligent decisions in competitive environments.

The Role of Alpha-Beta Pruning in Artificial Intelligence

In AI, alpha-beta pruning is most commonly associated with adversarial search problems, where two players are pitted against each other in a zero-sum game — one player’s gain is the other’s loss. The algorithm works alongside the minimax strategy to cut down on the number of game tree nodes that need to be evaluated, thereby allowing the AI to think more deeply and strategically within a limited time frame. A classic example is its application in Chess-playing AI programs, where a brute-force search through all possible moves and outcomes would be computationally infeasible. Alpha-beta pruning makes it possible for these systems to focus only on moves that matter, enhancing decision-making efficiency.

Application in Game Theory

Alpha-beta pruning fits perfectly within the framework of game theory, especially when applied to zero-sum games. In these scenarios, players make decisions by building game trees that represent every possible outcome of their moves. Game theory helps in understanding how players can optimize their strategies to gain a competitive edge. Alpha-beta pruning comes into play by pruning, branches in this game tree that would not alter the final decision of the players. For instance, in two-player board games like Chess or Go, each possible move can be represented as a tree, with each node indicating a potential state of the game. The pruning process eliminates irrelevant nodes, ensuring that computational resources are spent only on analyzing meaningful moves. This reduction in computational complexity makes it feasible to implement alpha-beta pruning in large-scale games with vast numbers of possible move combinations.

Core Concept: How Alpha-Beta Pruning Works

To understand how alpha-beta pruning works, it is essential to first grasp the minimax algorithm. Minimax evaluates the possible outcomes of a two-player game by alternating between a maximizer (one player trying to maximize their score) and a minimizer (the opponent trying to minimize the score). The algorithm works by exploring all potential game states and assigning values to them based on which player is winning. Alpha-beta pruning enhances this process by introducing two thresholds — alpha and beta — that help in cutting off unnecessary branches in the decision tree.

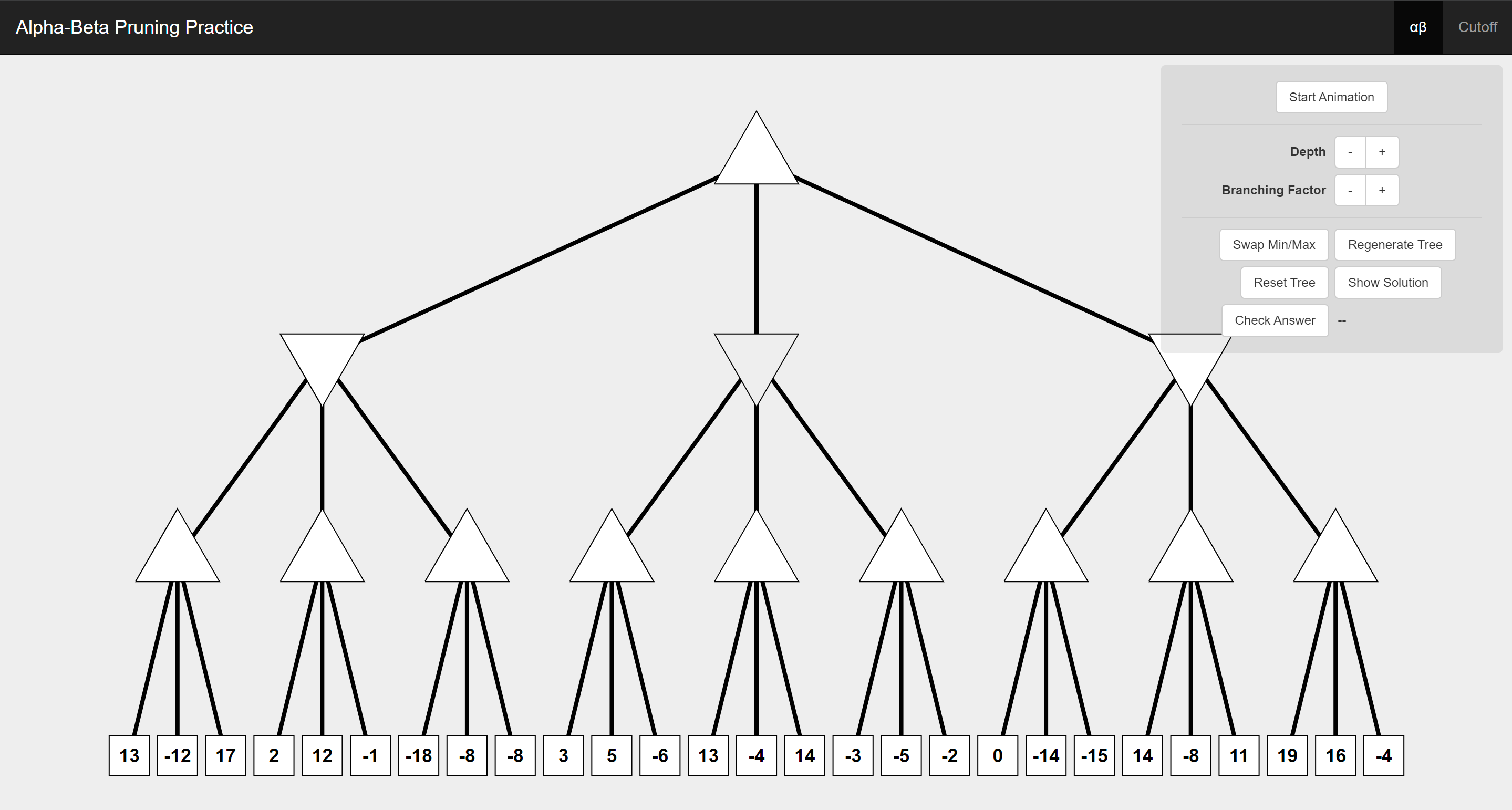Working of Alpha-Beta Pruning You can try visualizing this for yourself

Alpha represents the maximum score that the maximizer can guarantee, while beta represents the minimum score that the minimizer can ensure. As the tree is explored, if the current branch can’t provide a better outcome than the previously explored ones (as determined by alpha and beta), it is pruned. This allows the algorithm to skip large sections of the tree, speeding up decision-making without sacrificing the quality of the final result. The pruning reduces the number of nodes the algorithm evaluates, making it exponentially more efficient compared to a brute-force minimax search.

Alpha-Beta Pruning Implementation in Computer Science

In the context of computer science, alpha-beta pruning is a fundamental algorithm used to solve search problems that involve large branching trees. Implementing the algorithm typically requires a depth-first search strategy. The pruning process works best when nodes are evaluated in a specific order, such as from the most promising moves to the least promising ones. This optimizes the effectiveness of the pruning.

In terms of time complexity, the difference between using minimax alone and using minimax with alpha-beta pruning is substantial. For a minimax algorithm, the time complexity is {% katex inline %} O(b^d) {% endkatex %}, where “b” represents the branching factor (the number of possible moves at any point) and “d” is the depth of the tree. Alpha-beta pruning can reduce this to {% katex inline %} O(b^\frac{d}{2}) {% endkatex %}, effectively doubling the depth that can be searched within the same time constraints. This makes it indispensable for AI programs that require quick decision-making under time pressure, such as real-time strategy games.

Enhancing Algorithm Efficiency: Iterative Deepening

A technique commonly used alongside alpha-beta pruning is Iterative deepening, which further enhances the efficiency of the algorithm. Iterative deepening works by progressively deepening the search tree one layer at a time. The idea is that the algorithm first explores the shallowest parts of the tree and progressively works deeper, refining the alpha and beta values along the way. This approach allows for a more effective pruning process since the alpha and beta values are better informed by earlier, shallower searches.

By combining alpha-beta pruning with iterative deepening, AI systems can make better decisions with limited computational resources.

Alpha-Beta Pruning in Real-World AI Applications

In modern AI applications, aplha-beta pruning has been used in a variety of decision-making systems where adversarial conditions or optimization tasks are present. For instance, early versions of AlphaZero, a cutting-edge AI system developed by DeepMind, utilized alpha-beta pruning as part of its search strategy in games like Chess and Go. Though AlphaZero has evolved to use more advanced algorithms, alpha-beta pruning remains an essential building block in many game-playing AI systems. Beyond games, alpha-beta pruning can be found in areas like robotics, where machines must navigate through complex decision trees in real time, often in adversarial environments.

Alpha-Beta Pruning vs. Other Pruning Techniques

Although alpha-beta pruning is a powerful optimization technique, it is not the only method available. Other pruning techniques, such as Monte Carlo Tree Search (MCTS), are also popular in AI, especially in complex games like Go. MCTS relies on random sampling to explore potential moves rather than systematically evaluating every branch of the tree. While MCTS can be more efficient in certain situations, alpha-beta pruning remains more effective in deterministic, two-player games where all possible moves and outcomes can be predicted with reasonable accuracy.

Limitations of Alpha-Beta Pruning

Despite its many advantages, alpha-beta pruning has limitations. It is most effective in games or situations with a well-defined set of rules and outcomes, such as Chess or Checkers. However, in games with highly branching trees or uncertainty, like poker, where players must deal with hidden information and bluffing, alpha-beta pruning is less useful. Additionally, the efficiency of the algorithm depends heavily on the order in which nodes are evaluated. A poor move ordering can drastically reduce the effectiveness of pruning, resulting in longer computation times.

Enhancing Alpha-Beta Pruning with Heuristics

To further enhance the effectiveness of alpha-beta pruning, heuristics can be applied. In AI, heuristics are rules of thumb that help in decision-making by providing an estimate of the best possible move. In games like Chess, evaluation functions—heuristics designed to score a given board position—are often used to prioritize promising moves. By combining these heuristics with alpha-beta pruning, AI systems can search more intelligently, focusing their computational resources on the most critical parts of the game tree.

The Future of Alpha-Beta Pruning

As AI continues to evolve, alpha-beta pruning remains relevant, but newer algorithms are emerging that build on its principles. Techniques like neural networks, reinforcement learning, and MCTS are increasingly being used in tandem with or as alternatives to alpha-beta pruning. Nevertheless, the simplicity and effectiveness of alpha-beta pruning ensure its continued use in applications where fast and efficient decision-making is required.

Conclusion

Alpha-beta pruning is a fundamental technique in AI and game theory, offering a way to optimize decision-making by reducing unnecessary computation. Its history, from its early days in game trees to its modern applications in AI, highlights its importance in the development of efficient algorithms. By understanding how alpha-beta pruning works and how it fits into broader AI systems, we can appreciate its enduring relevance and potential for future advancements in AI-driven decision-making.

References for Further Reading

https://en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning

  • Sebastian Lague’s Chess Course

https://youtu.be/U4ogK0MIzqk?si=m5zN7rCsW0WsS-vM